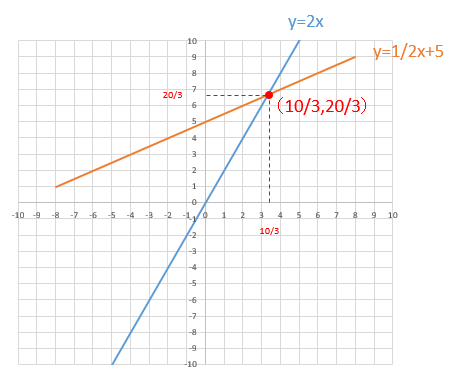
2直線の交点座標を連立方程式で求める方法 図解で超カンタンまとめ My Terrace マイテラス
連立方程式とグラフでaとbの交点Pの座標を求めなさいの問題があるんですが a → y=3X4 b → y=1/2X3 でこの連立方程式が解けません>< できたら加減法と代入法2つの解き方を教えてください; 連立方程式連立方程式の立て方に慣れるための練習問題(基礎1) 問題 シュークリームを個買おうと思っていたが,持っていたお金では140円足りなかったので, 18個買ったところ,1円余った。
連立方程式 グラフ 座標
連立方程式 グラフ 座標- 連立方程式を解かなければいけないですね。 一応やっておくと、求める直線を \(y=axb\) とおき、この直線が2点をどちらも通るので \(2=3ab\) \(6=5ab\) という二つの式が成り立つはずです。これらを同時に成り立たせる \(a,b\) が欲しいので連立方程式を解きます。連立方程式の解と グラフの交点の座標が 対応していることに注目! 大事なのは式とグラフの関係性 \
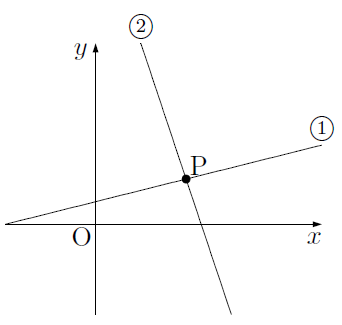
連立方程式とグラフ まなびの学園
一連の記事はこちら 図形と方程式1|座標の超基本「内分点」と「外分点」の計算 図形と方程式2|「方程式が表すグラフ」ってそもそも何? 図形と方程式3|直線の「傾き」の考え方を理解しよう! 図形と方程式4|一般の直線の方程式と平行・垂直条件 中2の連立方程式 文字を1つ消去して次元を下げる。その方法に (i)加減法、(ii)代入法がある。 ここでは、グラフ的見方で捉えてみます。 二元一次方程式⇒(変形)⇒ 一次関数 結論から言うと二元一次方程式 と一次関数 は同じである。連立方程式の解き方①(加減法) 1次関数のグラフの問題 ※1632〜の「グラフ→式を求める」 連立方程式の解き方②(代入法) ※1900〜のところ ※ 垂直二等分線/角の二等分線の図形的な意味 (参考) 2つの式(条件)を満たすのは「交点」ということ
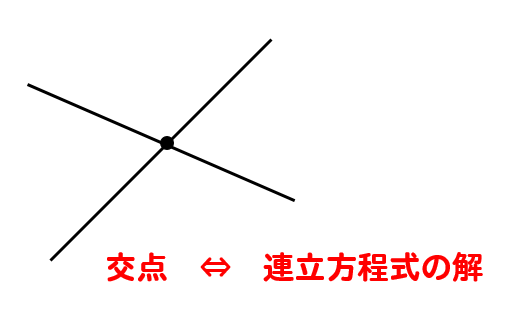
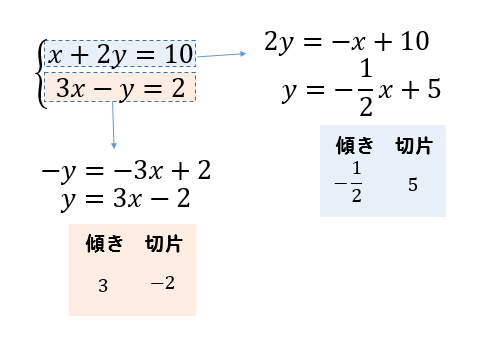
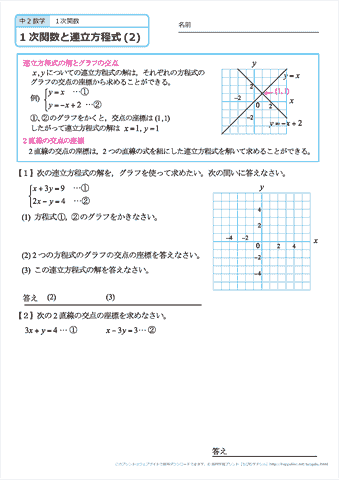
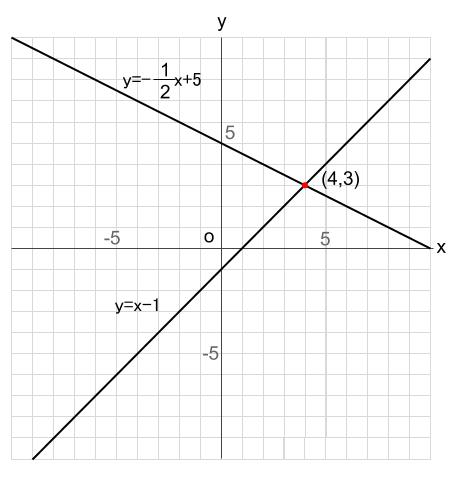
連立方程式を解く 次に連立方程式を解き、方程式を完成させます。 まず求める方程式は 。 この方程式に当てはまる、a と b を求める場合、 x と y に 座標(1, 1) と (5, 3) を代入して という連立方程式を立て、その解を求めてみます。 交点の座標は連立方程式を解くということ! 2つのグラフの交点を求める場合,それは連立方程式を解くということです。 先ほどの例題だと「円x 2 y 2 =10と円(x2) 2 (y1) 2 =5の交点の座標は(x,y)=(1,3),(3,1)」ということになります。連立方程式の解を求めることと同じです! つまり、 2 2 直線の交点は、 連立方程式 ⎧⎨⎩ y= x−1 y= −1 2x5 { y = x − 1 y = − 1 2 x 5 の解を求めることと一致します。 さきほど図示することで得た交点の座標 (4,3) ( 4, 3) が、 計算で求まります。 図示して
連立方程式 グラフ 座標のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
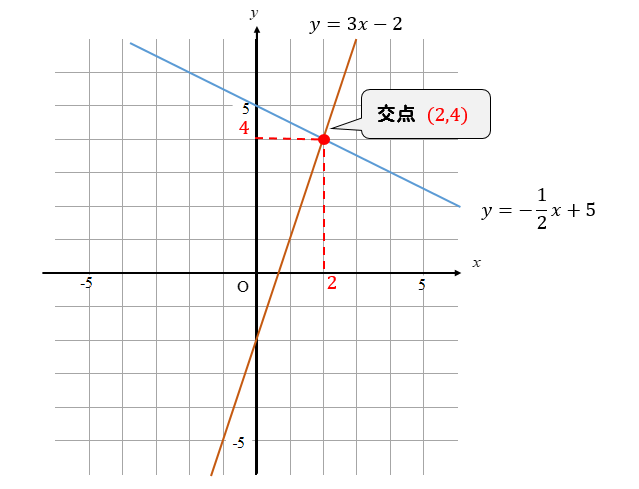 一次関数と連立方程式 1 ネット塾 | 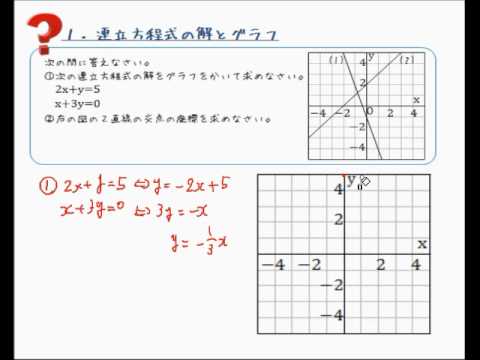 一次関数と連立方程式 1 ネット塾 | 一次関数と連立方程式 1 ネット塾 |
 一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 | 一次関数と連立方程式 1 ネット塾 |
 一次関数と連立方程式 1 ネット塾 | 一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |
「連立方程式 グラフ 座標」の画像ギャラリー、詳細は各画像をクリックしてください。
 一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |
一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |
 一次関数と連立方程式 1 ネット塾 | 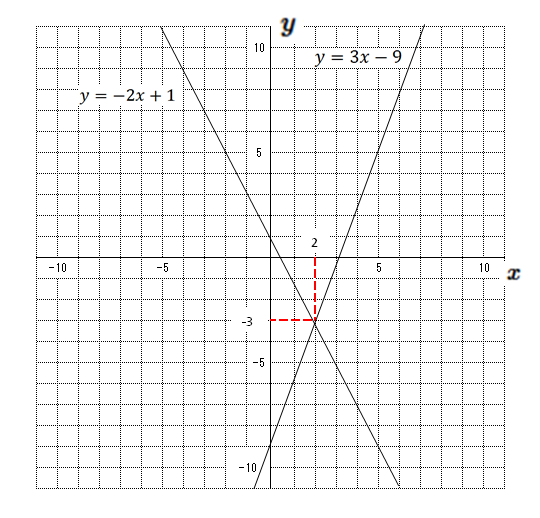 一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |
「連立方程式 グラフ 座標」の画像ギャラリー、詳細は各画像をクリックしてください。
 一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 | 一次関数と連立方程式 1 ネット塾 |
 一次関数と連立方程式 1 ネット塾 | 一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |
一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |
「連立方程式 グラフ 座標」の画像ギャラリー、詳細は各画像をクリックしてください。
 一次関数と連立方程式 1 ネット塾 | 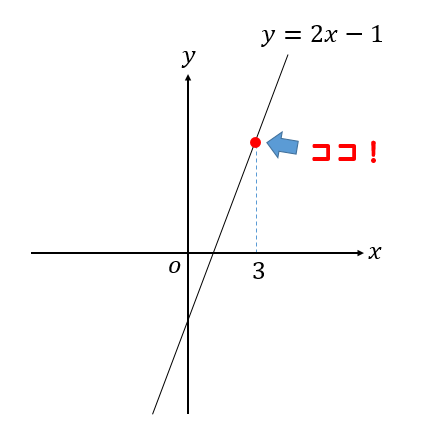 一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |
 一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 | 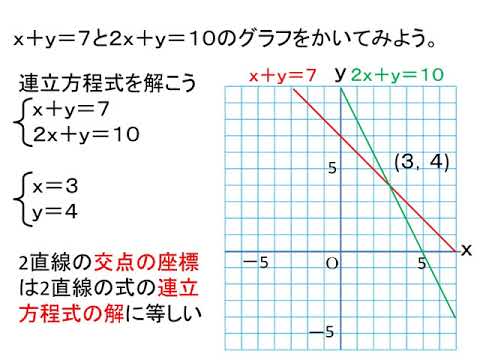 一次関数と連立方程式 1 ネット塾 |
 一次関数と連立方程式 1 ネット塾 | 一次関数と連立方程式 1 ネット塾 | 一次関数と連立方程式 1 ネット塾 |
「連立方程式 グラフ 座標」の画像ギャラリー、詳細は各画像をクリックしてください。
 一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 | 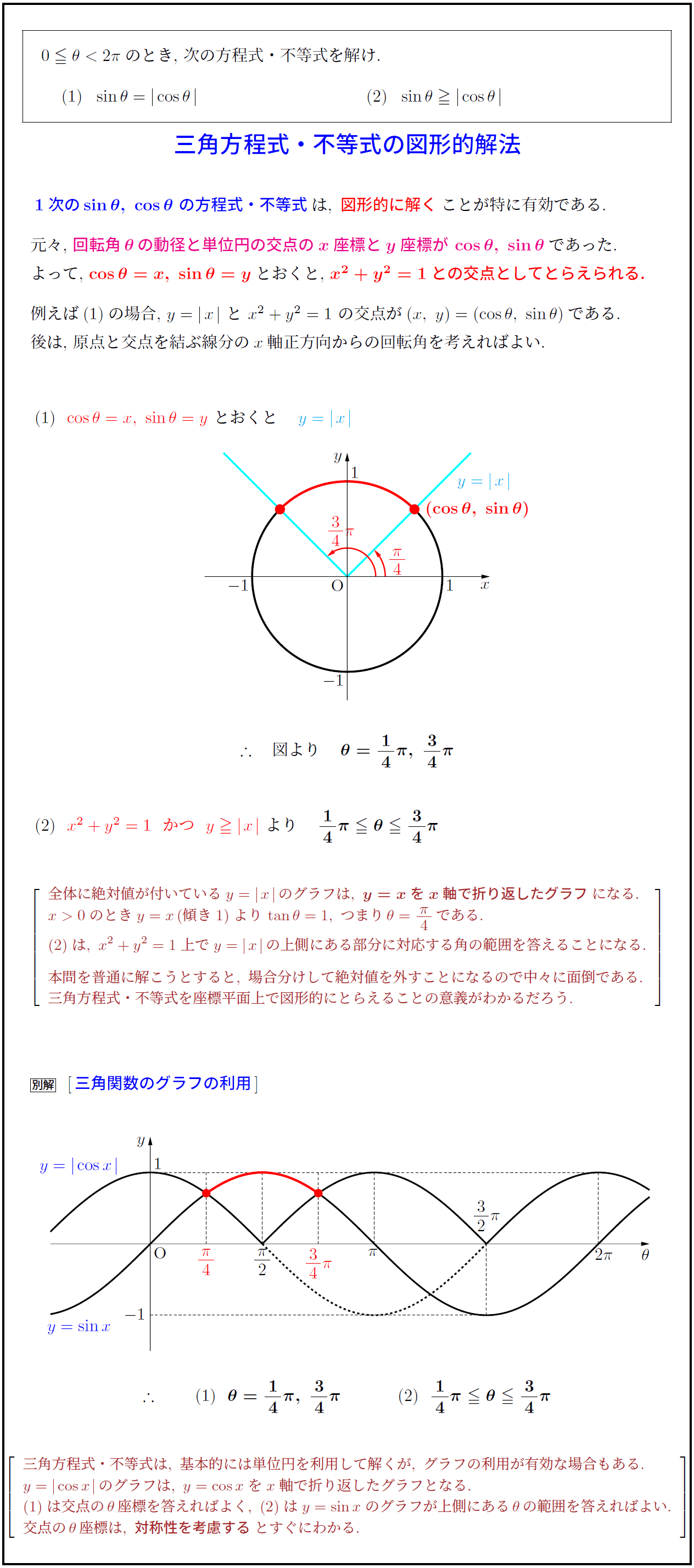 一次関数と連立方程式 1 ネット塾 |
 一次関数と連立方程式 1 ネット塾 | 一次関数と連立方程式 1 ネット塾 | 一次関数と連立方程式 1 ネット塾 |
 一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |
「連立方程式 グラフ 座標」の画像ギャラリー、詳細は各画像をクリックしてください。
 一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 | 一次関数と連立方程式 1 ネット塾 |
 一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |
 一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |
「連立方程式 グラフ 座標」の画像ギャラリー、詳細は各画像をクリックしてください。
 一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |
 一次関数と連立方程式 1 ネット塾 | 一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |
 一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |
「連立方程式 グラフ 座標」の画像ギャラリー、詳細は各画像をクリックしてください。
一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |
 一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 | 一次関数と連立方程式 1 ネット塾 |
 一次関数と連立方程式 1 ネット塾 | 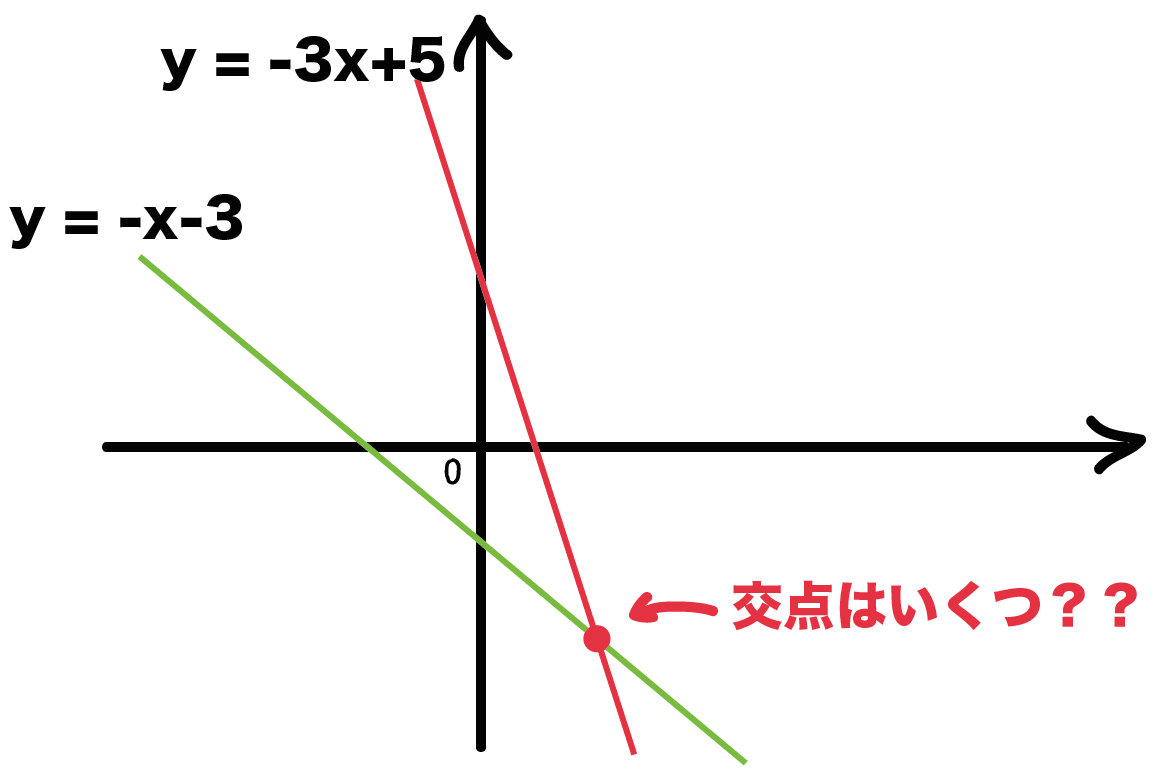 一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |
「連立方程式 グラフ 座標」の画像ギャラリー、詳細は各画像をクリックしてください。
 一次関数と連立方程式 1 ネット塾 | 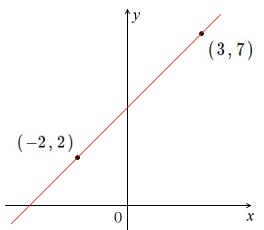 一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |
 一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 | 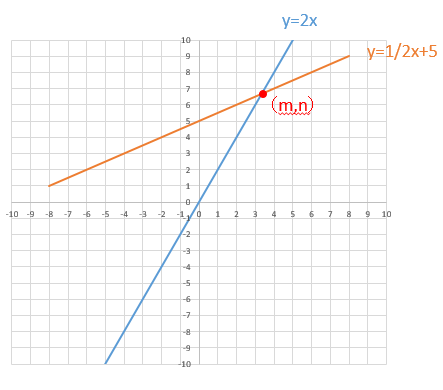 一次関数と連立方程式 1 ネット塾 |
 一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |
「連立方程式 グラフ 座標」の画像ギャラリー、詳細は各画像をクリックしてください。
一次関数と連立方程式 1 ネット塾 | 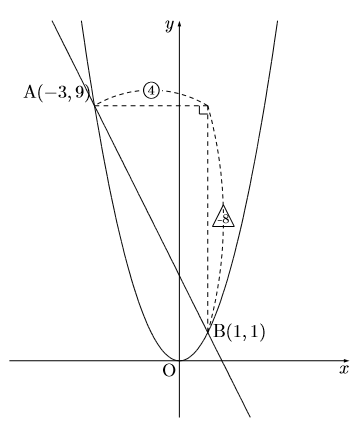 一次関数と連立方程式 1 ネット塾 | 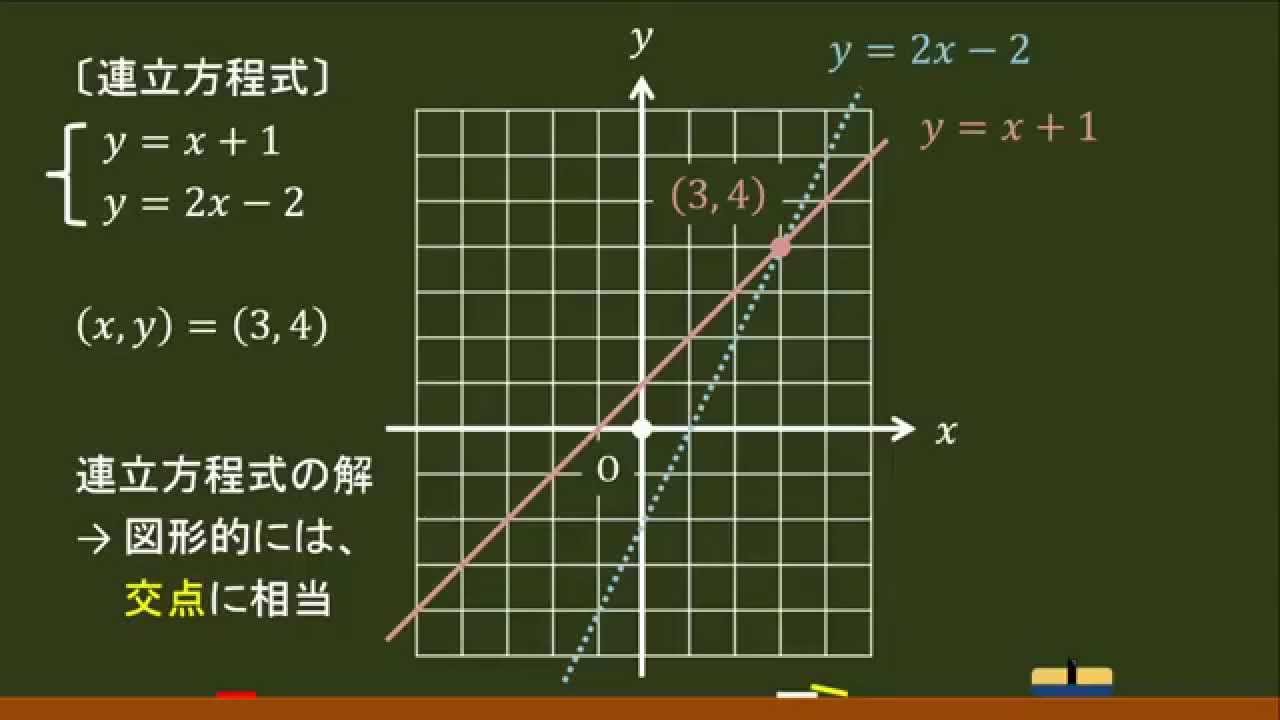 一次関数と連立方程式 1 ネット塾 |
 一次関数と連立方程式 1 ネット塾 | 一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |
 一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |
「連立方程式 グラフ 座標」の画像ギャラリー、詳細は各画像をクリックしてください。
 一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |
 一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |
 一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 | 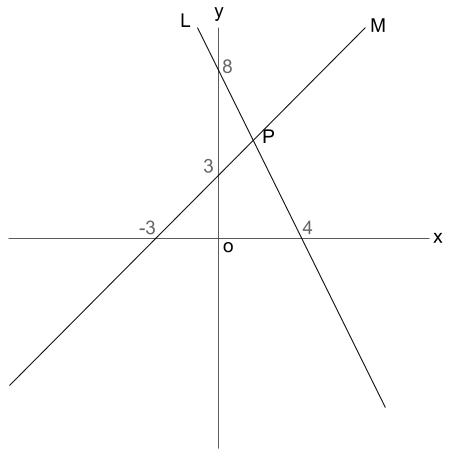 一次関数と連立方程式 1 ネット塾 |
「連立方程式 グラフ 座標」の画像ギャラリー、詳細は各画像をクリックしてください。
 一次関数と連立方程式 1 ネット塾 | 一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |
 一次関数と連立方程式 1 ネット塾 |  一次関数と連立方程式 1 ネット塾 |
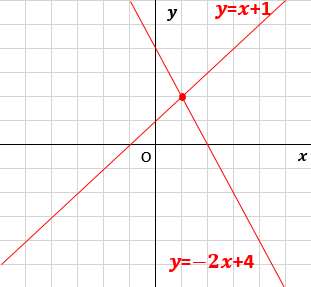
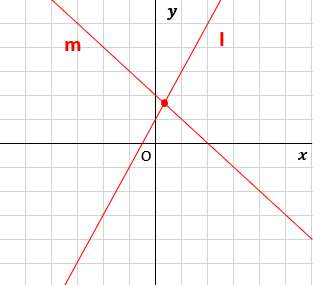
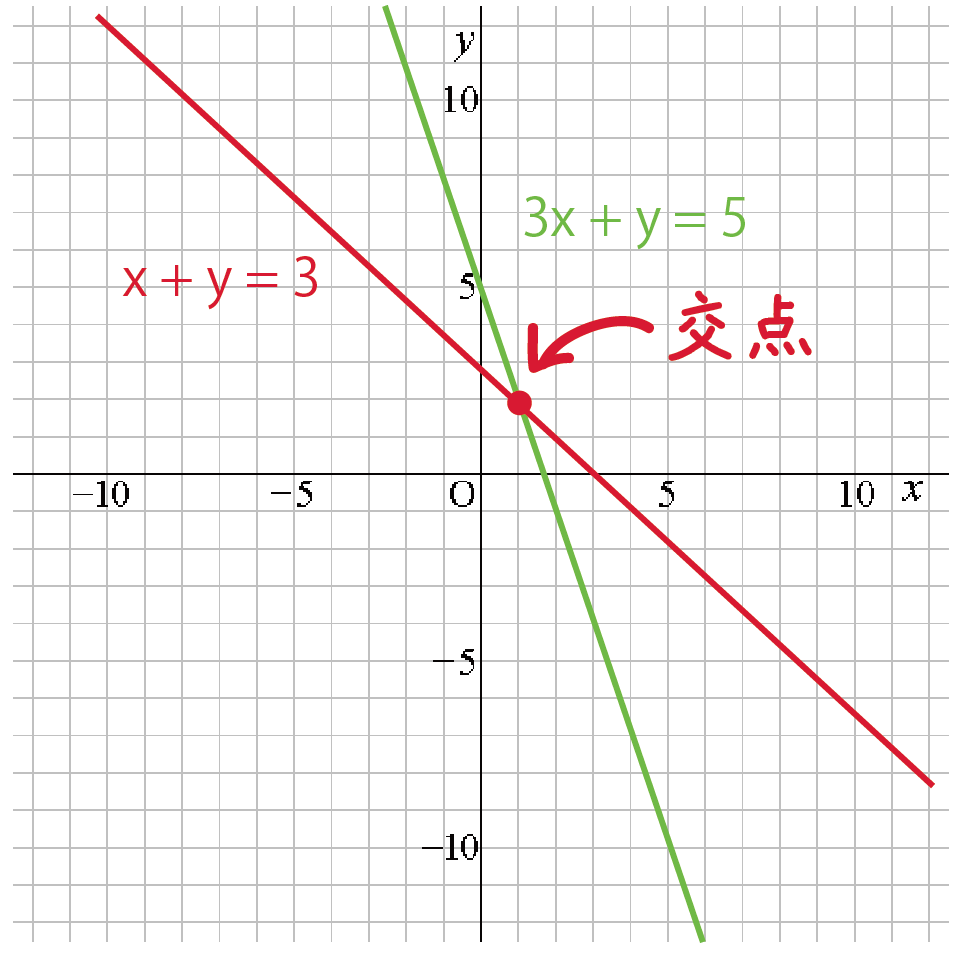
Y=2x1 のグラフですが、 このグラフ、実は 二元一次方程式 y=2x1 の解の集まりなのです。無数にある解1つ1つが座標上の点であり、その無数の点が集まって 線を構成しています。 そろそろ予想できてきた かもしれませんが、グラフ上の2本の直線(点の集まりアより,y=-3x-2 イより,y=x+2 グラフの 交点は(-1,1) x=-1,y=1 次の直線アとイの交点の座標を,計算で求めなさい。 3 ア y=2x+1 イ y=-x+4 連立方程式をつくると
Incoming Term: 連立方程式 グラフ 座標,




0 件のコメント:
コメントを投稿